何十年ぶりに数学の整数問題を解いてみました。
数式の入力方法が分からず、すべて画像のため読みづらいと思いますが、ご容赦ください。
問題
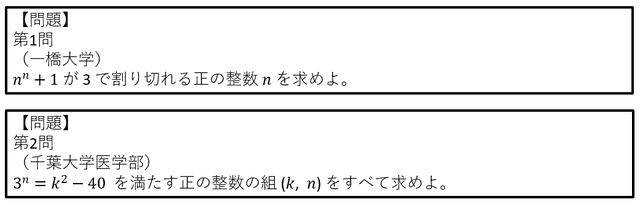
(一橋大学)
nn + 1 が 3 で割り切れる正の整数 n を求めよ。
(千葉大学医学部)
3n = k2 - 40 を満たす正の整数の組 (k, n) をすべて求めよ。
解答例



[第1問]
- A) n≡0 (mod 3) のとき
- nn+1 ≡ 0n+1 ≡ 0+1 ≡ 1 (mod 3) となり、常に3で割り切れないので不適。
- B) n≡1 (mod 3) のとき
- nn+1 ≡ 1n+1 ≡ 1+1 ≡ 2 (mod 3) となり、常に3で割り切れないので不適。
- C) n≡2 (mod 3) のとき
- nn+1 ≡ 2n+1 ≡ (-1)n + 1 (mod 3)
- このとき、nが偶数の時は常に3で割り切れないので不適だが、nが奇数の時は常に3で割り切れる
つまり、nが奇数でかつ3で割ったとき2余る数の時に題意を満たす。
よって、 n = 6k - 1 (kは正の整数)
[第2問]
与式を4で割ったときの余りを考える。
まず左辺を4で割ったときの余りは
3n ≡ (-1)n (mod 4)
となるため、nが奇数のときはnを4で割った余りは-1、nが偶数のときはnを4で割った余りは1。
次に右辺を4で割ったときの余りは
- kが奇数のとき(奇数の平方数を4で割ると必ず1余ることから)
- k2 - 40 ≡ 1 - 0 ≡ 1 (mod 4)
- kが偶数のとき(偶数の平方数を4で割ると必ず割り切れることから)
- k2 - 40 ≡ 0 - 0 ≡ 0 (mod 4)
よって、左辺と右辺が同値になるのは4で割ったときに1余るときのため、nは偶数、kは奇数と確定できる。
nは正の整数なので、aを正の整数とすると n=2a と表すことができ、与式を整理すると
k2 - 3n = k2 - 32a = (k + 3a) (k - 3a) = 40 = 23×5
kもaも正の整数のため、 k + 3a > k - 3a で k + 3a ≧ 4
(ので、負×負のパターンおよび小×大のパターンはない)
また、kは奇数なので k + 3a も k - 3a も偶数となる。
(ので、奇数を因数とする40×1 および 8×5のパターンもない)
このため、k + 3a = 20 かつ k - 3a = 2 の場合と k + 3a = 10 かつ k - 3a = 4 の場合に限られる。
- k + 3a = 20 かつ k - 3a = 2 の場合、 k=11 で 3a = 9 となり a=2
- k + 3a = 10 かつ k - 3a = 4 の場合、 k=7 で 3a = 3 となり a=1
n=2a なので、(k, n)= (11, 4), (7, 2)
説明





ともに倍数(約数)と余りに注目する問題です。
実は 問題1 は3で割った時の余りで場合分けする方針は立てたものの手も足も出ず、解答をカンニングしても式が理解できませんでした。
というのも私は文系でしたが行列をならった世代です。しかし、合同式なるものは習っていません。
いまは行列は習わないものの、合同式を使った整数問題の解法が受験数学では必須だそうです。
私と同じく合同式を知らない人のために説明します。
「7を3で割ると1余る」ということを 「 7=3k+1 」 と式に表せますが、合同式では
と表現できます。
正確に説明すると a≡b (mod 3) は、 a を3で割った余りと b を3で割った余りが等しいと意味しています。
この合同式の性質として、加・減・乗が可能(除は条件つきで可能)ということがあります。
具体的には、 a≡b≡c≡d (mod i) のとき(文字の条件は省略します)
が成り立つということです。
そして使い勝手がいいのが、
という性質です。
つまり、合同式においてはn乗の数字は、同じ余りとなる数に置き換えることができるということ、そして置き換えたn乗の数字が計算できる場合、乗数のnをはずすことができるということです。
この性質は両方の問題で使用しています。
しかし、倍数(約数)や余りに注目するということは、合同式で考えるだけではありません。
例えば ( 3x - 1 ) をみたときに「3で割ったときに-1余る数字」だと発想することが重要な時もあります。(整数問題のときだけです。)この発想は、背理法で矛盾を指摘する場合や場合分けの数をしぼりたい場合などに有効です。
また平方数を3または4で割ったときの余りにも特徴があります。
3で割ったときの余りをみてみます。
3の倍数の平方数が3で割り切れるのは自明でしょう。
3で割り切れない整数は 3k ± 1 と表すことができます。
この平方数は (3k±1)2 = 9k2 ± 6k + 1 = 3 ( 3k2 ± 2k ) + 1 となるため、必ず3で割ったとき1余ります。
つまり、平方数は3で割ると必ず余りが0か1になります。
4で割ったときの余りをみてみます。
偶数の平方数は (2k)2 = 4k2 なので、必ず4で割り切れます。
奇数の平方数は (2k+1)2 = 4k2 + 4k + 1 = 4 ( k2 + k ) + 1 なので、必ず4で割ったととき1余ります。
つまり、平方数は4で割ると必ず余りが0か1になります。
この特徴は 第2問 で利用しています。
[第1問]
王道の積の形にする解法は、nが奇数の時に因数分解することもできますが、nが偶数の時は因数分解できないため、難しそうです。
範囲をしぼる方針もnnが無限に大きくなるため、絞り込めそうにありません。
そのため、倍数(約数)と余りに注目する解法を検討します。
当然3で割ったときを検討するのですが、合同式は同じ余りを持つ数に置き換えできることと、 0n や 1n, (-1)n という計算可能な数字をうまく使います。
このとき、「3で割ったときに2余る」と「3で割ったときに-1余る」は同じだとわかれば、「2」を3で割ったときの余りと「-1」を3で割ったときの余りが同じだと発想を切り替えられるので、合同式上の置き換えができます。解答例では余りが2として置き換えていますが、最初から余りが-1として合同式を表現するほうが分かりやすいかもしれません。
[第2問]
この問題は平方数がある引き算なので、積の形にする方針として、「40」を無理やり平方数にしてみましょう。比較的近い平方数としては 62=36 と 72=49 がありますが、差分が3の倍数となる 49 を使って検討してみます。
k2 - 40 = 3n > 0 から、k ≧ 7
3n = k2 - 40 = k2 - 49 + 9 = ( k + 7 ) ( k - 7 ) + 9
よって、 3n - 9 = 32 ( 3n-2 - 1 ) = ( k + 7 ) ( k - 7 )
k≧7 から n≧2 となり、因数はすべて整数ですが、 3 と 3n-2-1 は互いに素であるもののパターンの絞り込みは大変そうです。
( 3n + 39 = 3 ( 3n-1 + 13 ) = ( k + 1 ) ( k - 1 ) なども同様 )
範囲をしぼりこむ解法も、 k2 も 3n も無限に大きくなるため、厳しいです。
というわけで、倍数(約数)と余りに注目する解法を検討します。
まず、偶数か奇数か(2で割ったとき)に注目すると k2 すなわち k は奇数でなくては与式の等式は成立しませんが、分かるのはこれだけです。
次に3で割ったときを検討します。
上記の通り、平方数を3で割ったときの余りは0か1です。
左辺の 3n は3で割り切れ、右辺の 40 は3で割ると1余るので、 k2 は3で割ると1余る数字でなくてはならず、 k は3で割り切れないことは分かります。
ただ、分かるのはここまででこれ以上の絞り込みはできそうにありません。
そのため、4で割ったときを検討したものが解答例です。
3は「4で割ると3余る」のですが、 第1問 と同様に「4で割ると-1余る」と言い換えることができるので、合同式を置き換えます。
平方数を4で割ったときの余りの特性から、偶数と奇数の場合分けでしぼりこみを行い、偶数にしぼりこめれば因数分解して積の形にすることができます。
k が奇数であることを利用して、効率よくしぼりこんでいきましょう。
ご質問は下の コメントを書く からお願いします。

